Hi-lining: some interesting info

  • Thread starter Thread starter Jack
  • Start date Start date
  • Replies Replies 50
  • Views Views 12K
I tie a bowline-on-a-bight in the suspension line, then girth hitch my friction saver into the double loop. It can be moved one way or the other per the main line (before putting weight in it of course), to set it at the desired deflection.
 
Yeah, good bump. At least he was a very fine looking fellow, if I couldn't understand a word he said; but the long and short that I got out was, "Jed... just don't rig like this ever. O.k, Bud... ever. And then you should be just fine."
 
Jed said:
Yeah, good bump. At least he was a very fine looking fellow, if I couldn't understand a word he said; but the long and short that I got out was, "Jed... just don't rig like this ever. O.k, Bud... ever. And then you should be just fine."
Click to expand...

:lol:
 
I'm really never in that big of a hurry to have to rig biiiiig chunks down, if i was in that big of a hurry i would just start the job yesterday.
 
rumination said:
Question: When setting up a high line in the past I have used prusiks to lock the position of my tie in on the high line in order to be suspended directly over the working area. This means that my load is not centered directly in the middle of the highline as it was in his demonstration. In this case would the load be different on the two anchor points or would it still be shared evenly? I assume that some basic trigonometry would tell me the answer, but I've forgotten all of that now
Click to expand...

Yes and no. Yes the load would be different on each anchor. No you can't use basic trig to solve it. Or I should say, trig is used in the process of solving it but it's a statics problem, you have to account for all of the forces involved. In a basic Y shaped rigging, you can get away with just using trig to solve because by symmetry, the tension in each leg is equal, T1 = T2.

When the load isn't in the center and the angles aren't equal, T1 and T2 are both unknown and can't be solved with one equation. Using statics, the forces are summed in each direction and yields the system of equations needed to solve for the tension in each leg.
 
Last edited:
Helluva first post! Statics, trig...cool you have an understanding of what is needed to cipher an answer. Pitch in whenever you can. Welcome to the House.
 
I always wanted to know more about the math end of it. I'm pretty good at visualizing the rigs I need and how they will act but it would be nice to see the math behind it.(for bragging rights of course )
 
Thanks guys. I haven't worked as an Arborist in about 10 yrs but thinking about doing some rec climbing and have been bouncing around looking at all the cool new SRT stuff. Anyway, I'm not an expert by any stretch but do have some physics/engineering knowledge that I can throw at question like this and maybe hash out an answer.

Edit: Page, I'll draw up a little diagram this eve or tomorrow to show how it's solved. The actual math in a simple statics problem isn't complicated, just basic trig and algebra. Drawing the free body diagram to get all of the forces accounted for is the trick. From there the math can be applied to set up the equations and solve for the unknown forces.
 
Here's an example problem I came up with of the attachment point being off center so there's two different rope angles. So to do that, all the forces pulling "up" (Y direction) are accounted for, 200 lbf is down so it's negative. Then all the forces pulling in the X direction are accounted for and T1 is negative since it's pulling left.

Once the two equations are set up, they can be solved quickly with a matrix in a calculator or done by hand the long way, solving for one then plugging it back in to the other.

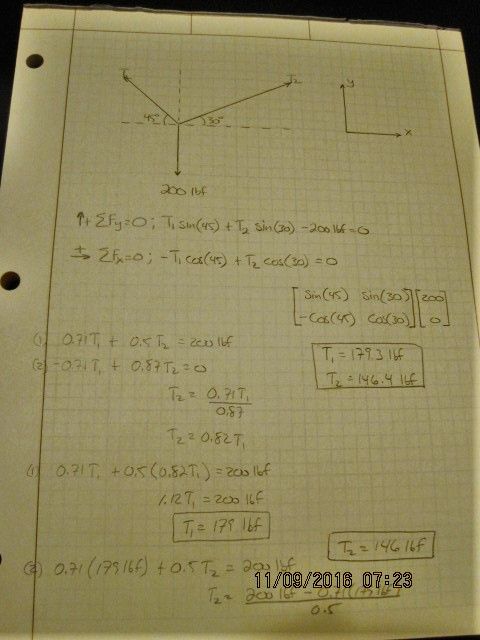
Off-center%20Y-rig_zpsnpvh1stg.jpg
 
Rumination said he wasn't sure if the loads are equal or not, with an offset from middle of the span.

Most things can be figured out by taking them to an extreme. e.g. If you hang a line 1000' wide, and load it 1' off an anchor, it's probably pretty intuitive that the two anchor loads are unequal. By how much?---that takes math.
 
Welcome!

My model on horizontal ridge line support is a similair 2:1 lift pulley system!
(unorthodox no schooling for this either)
Both legs of rope support for 2:1 are inline w/gravity flow;
0 degrees deflection from pure inline each leg of support.
.
1000#/ 2 supports = 500# upward needed on each leg
0degrees deflection, all of rope inline/usable for support
.
vs.
.
Pull both rope ends apart, pulley in center,
still 2 legs of support/sharing load
just each support leg is deflected from pure inline.
.
So, rope tension raises, as not all of rope tension usable for the inline support needed
another way to view is volume of force in rope vessel still needs to support load, but also contains pull across forces on spread supports.
Either way, rope tension to support same 1000# is now more than 2 legs of 500# each.
.
Half the spread angle of ropes is the deflection from inline for each leg of support(see calculator link)
half the load ÷ cosine of deflection = amount of line tension needed to support load
or half the load X secant of deflection(1/cosine of deflection)
.
calculated line tension x sine of deflection = pull across forces (not downward load force, spreading force).
calculated line tension x cosine of deflection = pull downward forces(1/2 of load; really just reversed formulae how got in 1st place);
.
.
.
On speed lines i always tried to bluff/ get low anchor farther back than target delivery area;
so didn't have to pull tightly to delivery area, but rather slop down/slack to deliver under less line tension.
If can have low, backfield anchor bluff 10' off ground even easier to slack down to real delivery area after dodging obstacle!
(like deliver to curb, but anchor across road 10' up, slacken line so delivers to original curb)
similarly can bluff high anchor higher, back; then run whole ride under less tension, by making it over qualified!
.
This, then birthed from that/above, so same math on angles etc.,
>> try to bluff wider than need so can slop under less tension, rather than maintain higher line tension to deliver to target:
.
drift_line.png


.
edit:
Calculator i made for showing force patterns: tinyurl.com/pulley-forces
(pulley on rope from vertical lines to centered on more horizontal spans)
 
Last edited:
theTreeSpyder said:
Pull both rope ends apart, pulley in center,
still 2 legs of support/sharing load
just each support leg is deflected from pure inline.
.
So, rope tension raises, as not all of rope tension usable for the inline support needed
another way to view is volume of force in rope vessel still needs to support load, but also contains pull across forces on spread supports.
Either way, rope tension to support same 1000# is now more than 2 legs of 500# each.
.
Half the spread angle of ropes is the deflection from inline for each leg of support(see calculator link)
half the load ÷ cosine of deflection = amount of line tension needed to support load
or half the load X secant of deflection(1/cosine of deflection)
.
calculated line tension x sine of deflection = pull across forces (not downward load force, spreading force).
calculated line tension x cosine of deflection = pull downward forces(1/2 of load; really just reversed formulae how got in 1st place);
Click to expand...

I see what you're saying. Unfortunately, doing it that way is going to lead to errors when the loads aren't symmetrical. You have the right idea, the tension of each leg has to be resolved into it's X/Y components. The trick is that ALL of the forces in the X and Y direction have to be accounted for in each equation. Can't just do one leg at a time. It makes sense intuitively, one leg has a certain amount of force pulling in the -X direction, and the other is pulling in the +X. They're pulling against each other, both contributing to the total amount of tension in the lines. If only one side is calculated at a time by itself, then the amount of additional tension in the line created by the other side pulling against it isn't accounted for.
 
In your drawing, you state that the truck will lose traction the farther it pulls without a lower pulley. Actually it seems that all things being equal, the farther the truck is from upper pulley and the more the angle is decreased, the more traction the truck would have, especially if pulling forward with a rear wheel drive vehicle. Correct me if I am wrong.
 
Brydan,
never went to school etc. on it.
But, hope this works for the matching calculator link with centered(i guess you say symmetrical) load etc. as pictured in Flash widget?:
mytreelessons.com/forcesPulley_verbose.swf
(that was to be included but got cut in an early morning edit i guess,sorry, so appended w/pic edit)
Certainly though load to one side, line on slant, motion dynamics, friction complicates matters beyond base model presented.
(Will play with load not at center calc page, thanx!)

***
Limbrat
The angle would be more favorable gradually, yes is fair.
(i'm looking at starting from slack, pulling forward)
.
The other part of that is the line tension, that here would trump?(damn said the T word)
If low redirect pulley at truck hitch height;
none of the line tension is lifting up on truck, so not decreasing traction to pull.
vs.
Any upward angle X increased line tension;
tends to lift up on rear of truck with part of line tension,
decreasing traction etc. is what i was trying to point out.
.
In this specific usage here; probably more of personal best practices/for most positive, predictable actions; and to illustrate principle
L-earned to put weight in back of truck, make sure solid, dry road, plenty of gas
and take in consideration of this type of upward angle pull,
like when pulling tree forward on hinge from high tie off etc.
.
Guess i could change that to as line tension increases(done),
was looking at starting from slack,
and the more you pull forward;
the more upward tension angle (less angle but more tension),
the less traction, as witnessed many times!
Thanx!
 
theTreeSpyder said:
Brydan,
never went to school etc. on it.
But, hope this works for the matching calculator link with centered(i guess you say symmetrical) load etc. as pictured in Flash widget?:
mytreelessons.com/forcesPulley_verbose.swf
(that was to be included but got cut in an early morning edit i guess,sorry, so appended w/pic edit)
Certainly though load to one side, line on slant, motion dynamics, friction complicates matters beyond base model presented.
(Will play with load not at center calc page, thanx!)
Click to expand...

That calculator looks fine to me. I didn't read everything on the page but get the same numbers.

I agree with you about the importance of the line angle tied to the truck. Lower angles make a big difference. If you could even get the block slightly lower than the attachment, then the traction gets better as the tension increases cause the tires are being pulled into the road
 
You must log in or register to reply here.

Similar threads

davidwyby
Launcher for rope? (Not throw line)
Replies
11
Views
391
SeanKroll
SeanKroll
Dopey
Need some equipment advice for my pruning job.
Replies
11
Views
814
Bermy
Bermy
Knotorious
Your Preferred Method for Flinging a Throw Weight/Throw Ball for Setting A Line!
Replies
10
Views
685
flushcut
flushcut
Treeaddict
Difficulty pulling a climb line up and over
2
Replies
45
Views
3K
Altissimus
Altissimus
Treeaddict
Throw line on your saddle
Replies
15
Views
1K
biggun
biggun
Back
Top